Quick sort là một thuật toán chia để trị. Quick Sort sẽ chọn một phần tử chốt(pivot) và phân thành 2 phần, một bên sẽ nhỏ hơn pivot và một bên lớn hơn pivot. Mỗi phân vùng được chia ra lại tiếp tục làm việc tương tự cho đến khi mảng không thể chia nhỏ hơn nữa thì quá trình sắp xếp kết thúc.
Chúng ta có rất nhiều cách chọn phần tử chốt, mình sẽ liệt kê 4 cách thường được dùng:
- Chọn phần tử đầu tiên trong mảng
- Chọn phần tử cuối cùng trong mảng
- Chọn phần tử ở giữa mảng
- Chọn random phần tử bất kỳ trong mảng
Mình sẽ mô tả từng bước cho phép sắp xếp tăng dần và chọn phần tử cuối làm phần tử chốt.
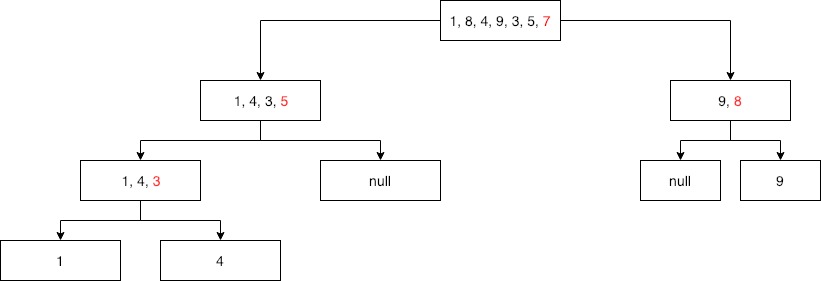
Trong thuật toán Quick Sort, điểm chính chúng ta cần lưu ý là thuật toán phân vùng dựa theo phần tử chốt(pivot), sau mỗi lần phân vùng trong khoảng [low – high] ta sẽ được một phân vùng mới [low – high] mà phần tử chốt của chúng ta chọn sẽ nằm giữa hai phân vùng nhỏ, một bên chứa tất cả các phần tử lớn hơn pivot và bên còn lại chứa tất cả các phần tử nhỏ hơn pivot.
public static <T extends Comparable<T>> int partition(T[] arr, int low, int high) {
T pivot = arr[high];
int i = low - 1; // lưu lại vị trí cuối cùng có giá trị nhỏ hơn phần tử chốt(pivot)
for (int index = low; index < high; index++) {
/*
* Use codition arr[j] with pivot
* Sort by ASC => Compare "<="
* Sort by DESC => Compare ">="
*/
/*
Biến i: lưu lại vị trí cuối cùng có giá trị nhỏ hơn phần tử chốt(pivot)
Biến: index: vị trí đang xét đến trong phần vùng [low - high]
Ý tưởng:
- Bắt đầu mặc định chưa tất cả các phần tử trong phần vùng đều lớn hơn pivot
- Duyệt từng phần tử trong phân vùng
+ nếu phần tử được xét nhỏ hơn hoặc phần tử chốt => tăng i lên 1, xét phần tử tiếp theo
+ nếu phần tử được xét lớn hơn phần tử chốt => xét phần tử tiếp theo
*/
if (arr[index].compareTo(pivot) <= 0) {
i++;
T temp = arr[i];
arr[i] = arr[index];
arr[index] = temp;
}
}
T temp1 = arr[i + 1];
arr[i + 1] = arr[high];
arr[high] = temp1;
return i + 1;
}
Sau khi hoàn thành được thuật toán phân vùng cho Quick Sort, Quick sort sẽ gọi đệ quy partition để hoàn thành việc sắp xếp mảng. Chúng ta sẽ có lần gọi partition chính như sau:
- Lần 1: Partition cho phân vùng lớn [low, high] => pi: index mới của pivot trong mảng
- Lần 2: Partition cho phần vùng bên trái [low, pi – 1 ]
- Lần 3: Partition cho phần vùng bên phải [low, pi +1 ]
public static <T extends Comparable<T>> void sort(T[] arr, int low, int high) {
if (low < high) {
int pi = partition(arr, low, high);
sort(arr, low, pi - 1);
sort(arr, pi + 1, high);
}
}
Minh hoạ Partition
arr[] = {1, 8, 4, 9, 3, 5, 7} low = 0, high = 6, pivot = 7
i = -1
j = 0, i = -1, arr[j] = 1: arr[j] < pivot => i = i + 1 = 0
swap arr[j] và arr[i] => arr[] = {1, 8, 4, 9, 3, 5, 7}
j = 1, i = 1, arr[j] = 8: arr[j] > pivot => bỏ qua.
j = 2, i = 1, arr[2] = 4: arr[j] < pivot => i = i + 1 = 2
swap arr[j] và arr[i] => arr[] = {1, 4, 8, 9, 3, 5, 7}
j = 3, i = 2, arr[3] = 9: arr[j] > pivot => bỏ qua
j = 4. i = 2, arr[4] = 3: arr[j] < pivot => i = i + 1 = 3
swap arr[j] và arr[i] => arr[] = {1, 4, 3, 9, 8, 5, 7}
j = 5, i = 3, arr[5] = 5: arr[j] < pivot => i = i + 1 = 4
swap arr[j] và arr[i] => arr[] = {1, 4, 3, 5, 8, 9, 7}
Cuối cùng swap pivot với arr[i + 1] và arr[high] => arr[] => {1, 4, 3, 5, 7, 9, 8}
Độ phức tạp
Độ phức tạp của thuật toán phụ thuộc rất nhiều vào phần tử chốt:
- Trường hợp xấu nhất: xảy ra khi quá trình paritition luôn chọn được phần tử lớn nhất hoặc nhỏ nhất: θ(n2)
- Trường hợp tốt nhất và trường hợp trung bình: chọn được phần tử có giá trị nằm khoảng giữa của đoạn, và lặp lại cho những lần phân trang tiếp theo: θ(nlog(n))
Link source code: