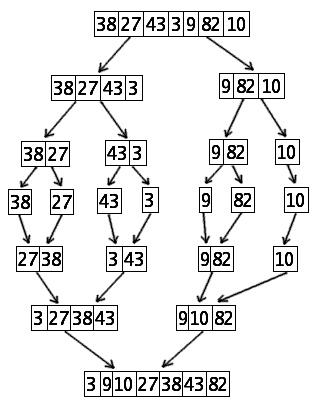
Merge Sort

Merge Sort là thuật toán chia để trị. Merge sort thực hiện bằng cách chia mảng thành 2 phần, mỗi phần như vậy lại gọi đệ quy để chia thành 2 phần con nhỏ hơn từ mỗi phần được tách ra, cứ như vậy cho đến khi mảng con không còn chia nhỏ được nữa(sub-array size = 1). Sau đó Merge sort tiến hành thu gon lại từ các mảng con một cách có thứ tự để được một mảng cuối cùng được sắp xếp.

Các bước chạy của Merge sort

Cho mảng arr[], Left: vị trí đầu muốn sắp xếp, Right: vị trí cuối cùng được sắp xếp.

Nguồn: Wikipedia

Implementation 

public static void merge(int[] arr, int l, int m, int r) {
        int i, j, k;
        int n1 = m - l + 1;
        int n2 = r - m;

        /* create temp arrays */
        int[] L = new int[n1];
        int[] R = new int[n2];
        /* Copy data to temp arrays L[] and R[] */
        for (i = 0; i < n1; i++)
            L[i] = arr[l + i];
        for (j = 0; j < n2; j++)
            R[j] = arr[m + 1 + j];

        /* Merge the temp arrays back into arr[l..r]*/
        i = 0; // Initial index of first subarray
        j = 0; // Initial index of second subarray
        k = l; // Initial index of merged subarray
        while (i < n1 && j < n2) {
            /*
             * Use codition L[i] with R[i]
             * Sort by ASC => Compare "<"
             * Sort by DESC => Compare ">"
             */
            if (L[i] <= (R[j])) {
                arr[k] = L[i];
                i++;
            } else {
                arr[k] = R[j];
                j++;
            }
            k++;
        }

        /* Copy the remaining elements of L[], if there are any */
        while (i < (n1)) {
            arr[k] = L[i];
            i++;
            k++;
        }

        /* Copy the remaining elements of R[], if there are any */
        while (j < (n2)) {
            arr[k] = R[j];
            j++;
            k++;
        }
    }

    public static void sort(int[] arr, int l, int r) {
        if (l < r) {
            // Same as (l+r)/2, but avoids overflow for
            // large l and h
            int m = l + (r - l) / 2;

            // Sort first and second halves
            sort(arr, l, m);
            sort(arr, m + 1, r);

            merge(arr, l, m, r);
        }
    }

Độ phức tạp

Số lần lặp để phân phối là θ(Log(n)), Hợp nhất 2 mảng nhỏ lại là một thuật toán đệ quy và có độ phức tạp θ(n). Tổng kết lại Merge sort có độ phức tạp θ(nlog(n)).

Link source code: Mergesort