Heap sort

Heap sort là thuật toán sắp xếp dựa trên việc so sánh các phần tử và dựa trên cấu trúc dữ liệu Binary Heap.

Cây nhị phân là gì?

Cây nhị phân là một cấu trúc dữ liệu mà trong đó mỗi node có nhiều nhất là hai nốt con, gọi là con trái và con phải. 

Binary Heap

Binary heap là một cấy nhị phân mà trong đó các node được lưu trữ sao cho mỗi nút cha đều lớn hơn các nút con của chúng(mỗi node cha có tối đa 2 con). Binary heap có thể biểu diễn bằng cây nhị phân hoặc bằng mảng.

Biểu diễn binary heap bằng mảng

Cho mảng arr[] có số lượng phần tử là N. Ta có, mỗi nút tại vị trí i( 0 <= i < n/2) có

• Node con trái tại vị trí 2 * i + 1
• Node con phải tại vị trí 2 * i + 2

Các bước chạy của heap sort cho sắp xếp tăng dần

1. Xây dựng một max heap từ input data.
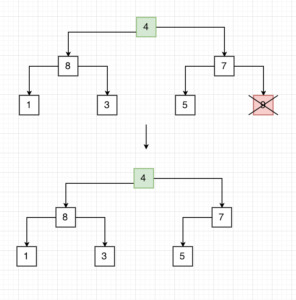
2. Sau khi build một max heap, phần tử đầu tiên trong heap là phần tử lớn nhất, swap phần tử đầu tiên với phần tử cuối để đưa phần tử lớn nhất về cuối mảng, sau đó rút gọn heap đi 1 và tái cấu trúc heap tại vị trí 0 .
3. Lặp laị bước 2 nếu size heap > 1

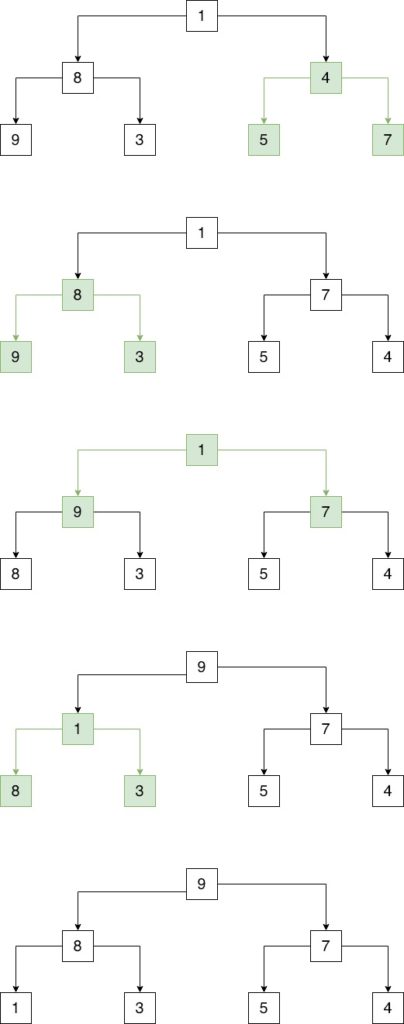
Build heap

arr[] = {1, 8, 4, 9, 3, 5, 7}

Sau khi build binary heap như trên, nhận thấy rằng phần tử đầu tiên trong mảng là phần tử lớn nhất. Ta thực hiện swap phần tử đầu tiên với phần tử cuối cùng của mảng.

Sau khi swap phần tử đầu tiên với phần tử cuối cùng của mảng. Ta tái cấu trúc heap tại vị trí 0, vì vị trí này được swap với phần tử lớn nhất ở bước nhất. 

Implementation

Heapify dùng để cấu trúc một cây con trong binary heap sao cho node cha luôn lớn hơn 2 node con.

public static <T extends Comparable<T>> void heapify(T[] arr, int n, int i) {
        int largest = i; // Initialize largest as root
        int l = 2 * i + 1; // left = 2*i + 1
        int r = 2 * i + 2; // right = 2*i + 2

        /*
         * Use codition both if
         * Sort by ASC => Compare ">"
         * Sort by DESC => Compare "<"
         */
        // If left child is larger than root
        if (l < n && arr[l].compareTo(arr[largest]) > 0)
            largest = l;

        // If right child is larger than largest so far
        if (r < n && arr[r].compareTo(arr[largest]) > 0)
            largest = r;

        // If largest is not root
        if (largest != i) {
            T swap = arr[i];
            arr[i] = arr[largest];
            arr[largest] = swap;

            // Recursively heapify the affected sub-tree
            heapify(arr, n, largest);
        }
    }

Sort sẽ build max heap, thực hiện chuyển phần tử lớn nhất về vị trí cuối mảng , sau đó tái cấu trúc heap với số lượng phần tử giảm đi 1.

public static <T extends Comparable<T>> void sort(T[] arr) {
        int n = arr.length;

        // Build heap (rearrange array)
        for (int i = n / 2 - 1; i >= 0; i--)
            heapify(arr, n, i);

        // One by one extract an element from heap
        for (int i = n - 1; i >= 0; i--) {
            // Move current root to end
            T temp = arr[0];
            arr[0] = arr[i];
            arr[i] = temp;

            // call max heapify on the reduced heap
            heapify(arr, i, 0);
        }
    }

Độ phức tạp của heap là θ(nlog(n)).

Link soure code: Heapsort