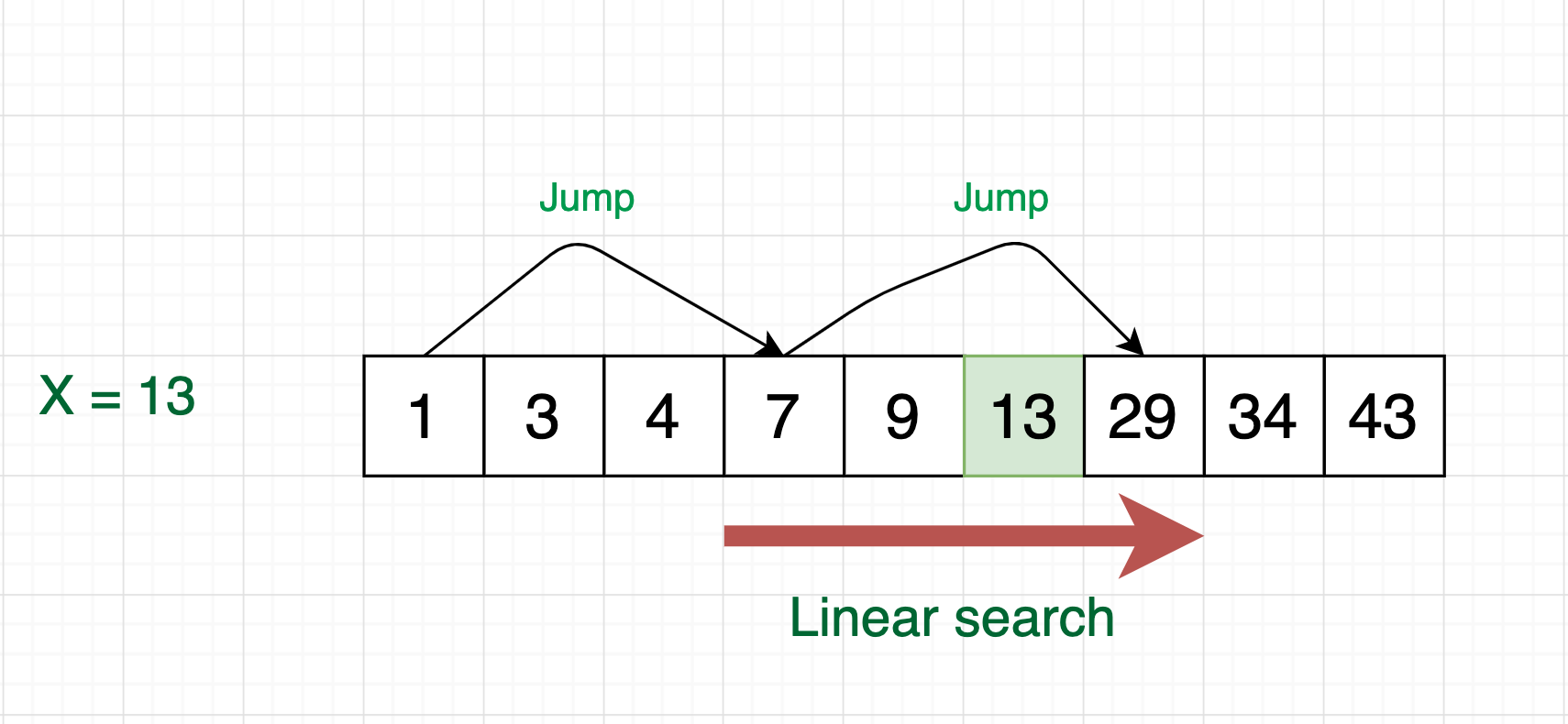
Giống như Binary Search Jump Search là một thuật toán tìm kiếm trên mảng đã được sắp xếp.
Ý tưởng của Jump Search là làm sao để giảm kiểm tra các phần tử ít hơn bằng cách nhảy về phía trước một khoảng các cố định để bỏ qua một số phần tử.
Ví dụ: Cho mảng arr[] có size là n và bước nhảy là m. Chúng ta sẽ tìm các phần tử tại vị trí arr[0], arr[m], arr[2m]… arr[km] cứ thế cho đến khi chúng ta tìm được khoảng k (k >=0) thoả arr[km] < x < arr[(k + 1)m], chúng ta sẽ thực hiện Linear Search từ vị trí km đến (k+1)m để tìm ra phần tử X.
Thực hành: Chúng ta có mảng arr[] = {0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610)}, n = 16, X = 55. Giả sử bước nhảy là 4. Chúng ta có
| B1: Nhảy từ 0 đến 4 -> không thoả arr[km] < x < arr[(k + 1)m] B2: Nhảy từ 4 sang 8 -> không thoả arr[km] < x < arr[(k + 1)m] B3: Nhảy từ 8 sang 12 -> thoả arr[km] < x < arr[(k + 1)m] B4: Thực hiện Linear Search từ 9 đến 12 để tìm X = 55 |
Implement
import java.util.*;
public class Main {
static int jumpSearch(int arr[], int x, int n)
{
// So khoang cach nhay
int step = (int)Math.sqrt(n);
// Tim kiem khoang k thoa arr[km] < x < a[(k+1)m]
int prev = 0;
while (arr[Math.min(step, n)-1] < x)
{
prev = step;
step += (int)Math.sqrt(n);
if (prev >= n)
return -1;
}
// Thuc hien linear search
while (arr[prev] < x)
{
prev++;
// Neu khong tim thay trong khoang km -> (k+1)m
if (prev == Math.min(step, n))
return -1;
}
if (arr[prev] == x)
return prev;
return -1;
}
public static void main(String[] args) {
int arr[] = { 0, 1, 1, 2, 3, 5, 8, 13, 21,
34, 55, 89, 144, 233, 377, 610 };
int x = 55;
int n = arr.length;
int index = jumpSearch(arr, x, n);
System.out.println(index != -1 ? index : "Khong tim thay");
}
}
Output: 10
độ phức tạp: O(√n)
Note: Kích thước tối ưu cho mỗi bước nhảy là √n, với cách tính này sẽ làm cho độ phức tạp của Jump Search là O(√n).