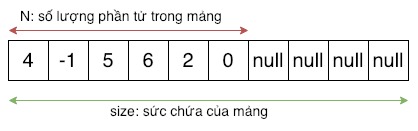
Viết chương trình tìm phần tử X trong mảng tăng dần, không cho biết số lượng phần tử.
Như hình trên, thì N chúng ta sẽ không được biết, chúng ta chỉ biết được sức chứa của mảng là size.
Ở đây, mình sẽ dùng kiểu Integer, thay vì sử dụng kiểu dữ liệu nguyên thuỷ int. Lý do là vì mảng int khi khởi tạo sẽ tự động gán các giá trị của mảng bằng 0, việc này sẽ ảnh hưởng đến kết quả tìm kiếm .
Cách 1: Linear search
Để sử dụng linear search, chúng ta cũng cần custom lại một tý để tránh duyệt hết các phần tử chưa được khởi tạo.
Sử dụng linear search sẽ tốn θ(n).
public class Main {
public static void main(String[] args) {
Integer[] arr = new Integer[1000];
int n = 50; // We don't know number of element in array => hide
// init array sorted ascending
for (int i = 0; i < n; i++) {
arr[i] = i;
}
int pos = linearSearch(arr, 25);
if (pos == -1) {
System.out.println("Not found");
} else {
System.out.println("Element found at: " + pos);
}
}
public static int linearSearch(Integer[] arr, int value) {
for (int i = 0; i < arr.length; i++) {
if (arr[i] == null)
return -1;
if (arr[i] == value)
return i;
}
return -1;
}
}
Output: Element found at 25
Cách 2: Binary search
Binary search hoạt động tìm kiếm trong một khoảng [a, b] được sắp xếp, Khi tìm kiếm trong mảng, thì a là vị trí phần tử đầu tiên của mảng, b là vị trí phần tử cuối cùng.
Nhưng, chúng ta không biết được b, mà chúng ta chỉ biết sức chứa của mảng là size. :-P. Mình sẽ áp dụng binary search cho khoảng [0, size – 1] vì mình chỉ biết được size thôi =)). Những phần tử chưa được khởi tạo mình sẽ xem nó như là một số rất lớn, rồi áp dụng binary search.
Sử dụng binary search sẽ tốn θ(Log(n)).
1: Khởi tạo
+ L = vị trí đầu tiên của khoảng tìm kiếm.
+ R: phần tử cuối cùng của khoảng tìm kiếm.
B2: Trong khi L <= R: middle = L + (R - L) / 2
+ Nếu arr[middle] > X || arr[middle] == null: R = middle - 1
+ Nếu arr[middle == X: return middle
+ Nếu arr[middle] < X: L = middle + 1
B3: return -1 nếu không tìm thấy
public class Main {
public static void main(String[] args) {
Integer[] arr = new Integer[1000];
int n = 50; // We don't know number of element in array => hide
// init array sorted ascending
for (int i = 0; i < n; i++) {
arr[i] = i;
}
int pos = binarySearchCustom(arr, 25);
if (pos == -1) {
System.out.println("Not found");
} else {
System.out.println("Element found at: " + pos);
}
}
public static int binarySearchCustom(Integer[] arr, int value) {
int l = 0, r = arr.length - 1;
while (l <= r) {
int m = l + (r - l) / 2;
if (arr[m] == null || arr[m] > value) {
r = m - 1;
} else if (arr[m] == value) {
return m;
} else {
l = m + 1;
}
}
return -1;
}
}
Output: Element found at 25
Link source-code: source
Nguồn tham khảo: geeksforgeeks