Tìm kiếm, thêm, xoá phần tử trong mảng đã được sắp xếp

Mục lục

1 Tìm kiếm
2 Thêm
3 Xoá

Trong bài biết này, chúng ta sẽ cùng nhau thảo luận về tìm kiếm, thêm. xoá phần tử trong mảng đã được sắp xếp.

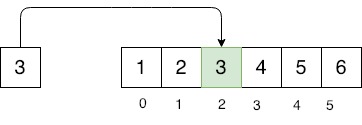
Tìm kiếm

Một mảng đã được sắp xếp thì chúng ta có thể tìm kiếm bằng phương pháp tìm kiếm nhị phân.

public class Main {

    public static void main(String[] args) {
        int[] arr = {1,2,3,4,5,6};
        int n = arr.length;
        int key = 3;
        int pos = binarySearch(arr, 0, n, key);
        if (pos == -1) {
            System.out.println("Khong tim thay");
        } else {
            System.out.println("Tim thay tai vi tri: " + pos);
        }
    }

    // binary search
    static int binarySearch(int arr[], int low, int high, int key)
    {
        if (high < low)
            return -1;

        int mid = (low + high)/2;
        if (key == arr[mid])
            return mid;
        if (key > arr[mid])
            return binarySearch(arr, (mid + 1), high, key);
        return binarySearch(arr, low, (mid -1), key);
    }
}

Output: Tim thay tai vi tri: 2

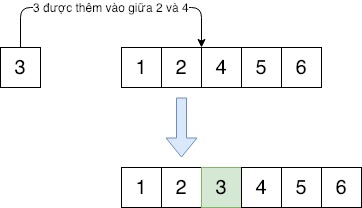
Thêm

Để thêm một phần tử vào mảng đã được sắp xếp, ta phải tìm kiếm vị trí thích hợp để thêm sao cho không làm mất trật tự đã được sắp xếp trước đó,

public class Main {

    public static void main(String[] args) {
        int arr[] = new int[20];
        arr[0] = 1;
        arr[1] = 2;
        arr[2] = 4;
        arr[3] = 5;
        arr[4] = 6;
        int size = arr.length;
        int n = 5;
        int key = 3;

        System.out.print("\nTruoc khi them: ");
        for (int i=0; i<n; i++)
            System.out.print(arr[i] + " ");

        // Inserting key
        n = insert(arr, n, key, size);

        System.out.print("\nSau khi them: ");
        for (int i=0; i<n; i++)
            System.out.print(arr[i] + " ");
    }


    static int insert(int[] arr, int n, int key, int size)
    {
        if (n >= size)
            return n;

        int i;
        for (i=n-1; ( i >= 0  && arr[i] > key); i--)
            arr[i+1] = arr[i];

        arr[i+1] = key;

        return (n+1);
    }
}

Output:
Truoc khi them: 1 2 4 5 6
Sau khi them: 1 2 3 4 5 6

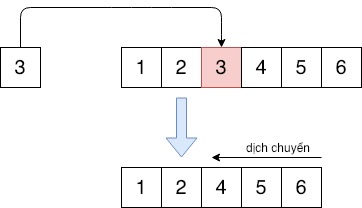
Xoá

Để xoá một phần tử trong mảng, sử dung binary search để tìm vị trí của phần tử cần xoá nằm trong mảng(pos), sau đó tiến hàng dịch chuyển các phần tử từ vị trí pos + 1 sang trái.

public class Main {

    public static void main(String[] args) {
        int i;
        int arr[] = {1, 2, 3, 4, 5, 6};

        int n = arr.length;
        int key = 3;

        System.out.print("Truoc khi xoa: ");
        for (i = 0; i < n; i++)
            System.out.print(arr[i] + " ");

        n = delete(arr, n, key);

        System.out.print("\nSau khi xoa: ");
        for (i = 0; i < n; i++)
            System.out.print(arr[i] + " ");
    }

    static int delete(int arr[], int n, int key) {
        int pos = binarySearch(arr, 0, n - 1, key);

        if (pos == -1) {
            System.out.println("Khong tim thay phan ");
            return n;
        }

        int i;
        for (i = pos; i < n - 1; i++)
            arr[i] = arr[i + 1];

        return n - 1;
    }

    // binary search
    static int binarySearch(int arr[], int low, int high, int key) {
        if (high < low)
            return -1;

        int mid = (low + high) / 2;
        if (key == arr[mid])
            return mid;
        if (key > arr[mid])
            return binarySearch(arr, (mid + 1), high, key);
        return binarySearch(arr, low, (mid - 1), key);
    }
}

Output:
Truoc khi xoa: 1 2 3 4 5 6
Sau khi xoa: 1 2 4 5 6